The seven bridges of Königsberg posed a mathematical problem, which was finally resolved by Leonhard Euler in the 18th century. His resolution laid the foundations of graph theory.

Kneiphof island is part of the city of Königsberg. The river Pregel flows around the island and splits into two arms. Seven bridges cross the river and somebody once asked whether it was possible to walk through the city and cross every bridge only once. 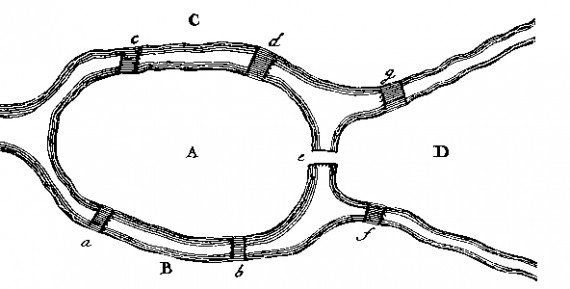Applying mathematics, Euler could showed two things:

1. The choice of route inside each land mass was irrelevant. Only the sequence of bridges crossed mattered.
2. It was not possible to cross every bridge only once when taking a walk through the city. This would have required an even number of bridges on each shore. However, the shores of Königsberg were accessible by an uneven number of bridges.

Read our next riddle: The Silk Road